ECC椭圆加密曲线

椭圆曲线的定义

Z_p(p>3)上的椭圆曲线指满足以下条件的所有对(x,y) ∈ Z_p 的集合：

​ y² ≡ x³ + a*x + b mod p

以及一个无穷大的虚数点此处记为G，其中（a,b）∈ Z_p

且满足条件4*a³ + 27*b² ≠ 0 mod p。

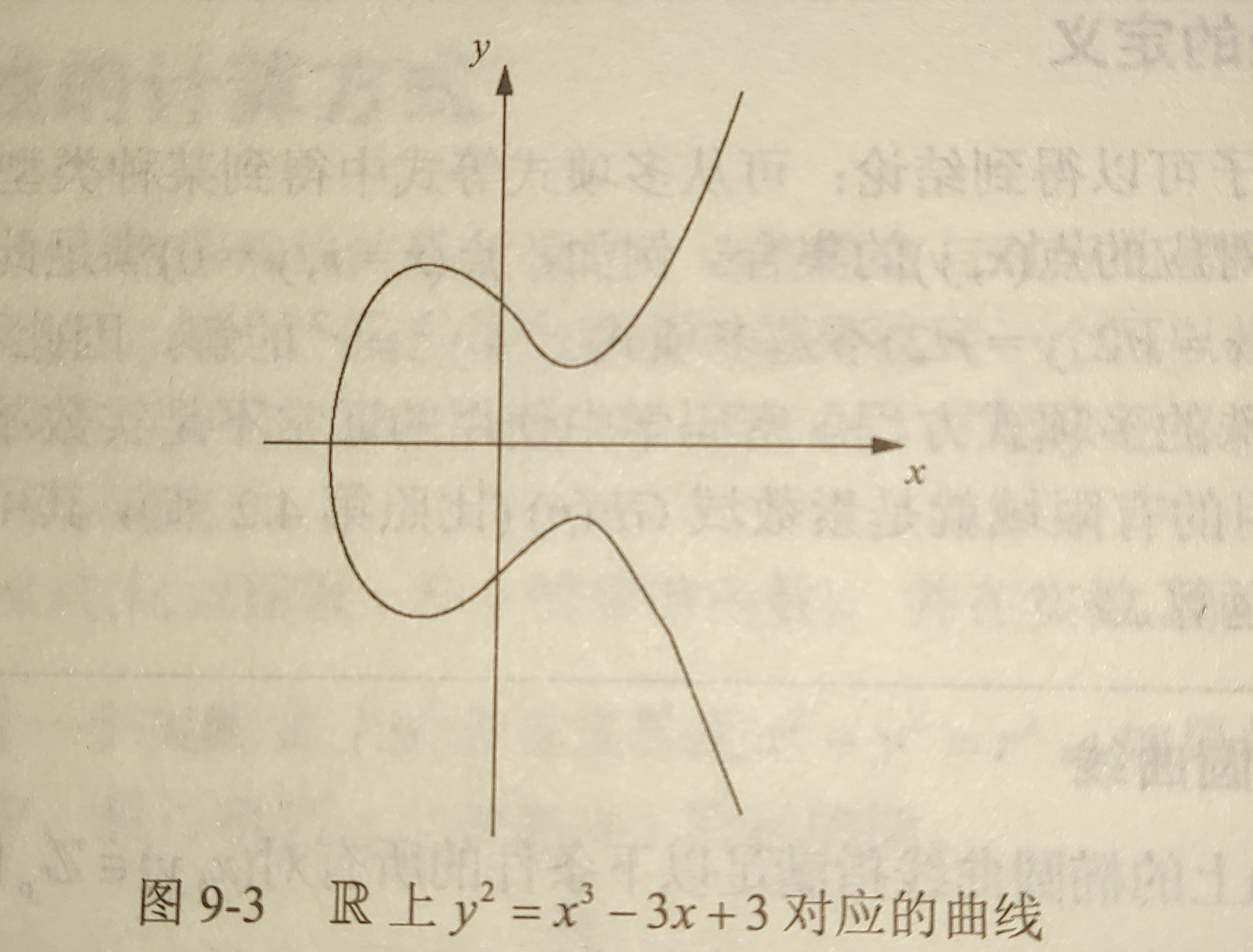
椭圆曲线上的群操作

可以用加法符号”+“来表示群操作，两点相“加”得到第三点

P + Q =R

即(x₁ , y₁ ) + (x₂ , y₂) = (x₃ , y₃)

两点相“加”的方式与这两点是否是相同点有关

相异点连线的交点并关于X轴对称的点即为得到的点：

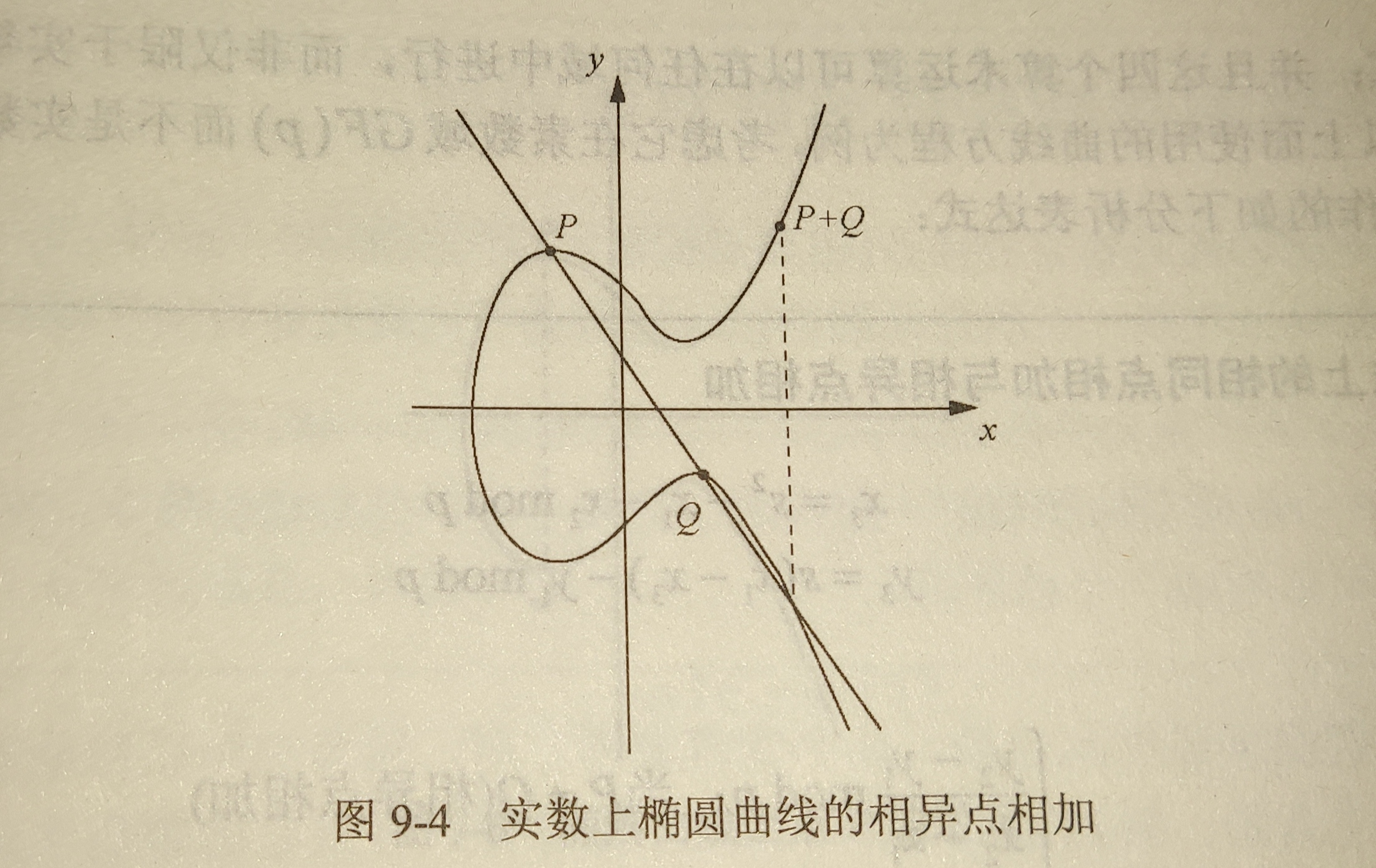
相同点切线的交点取对称：

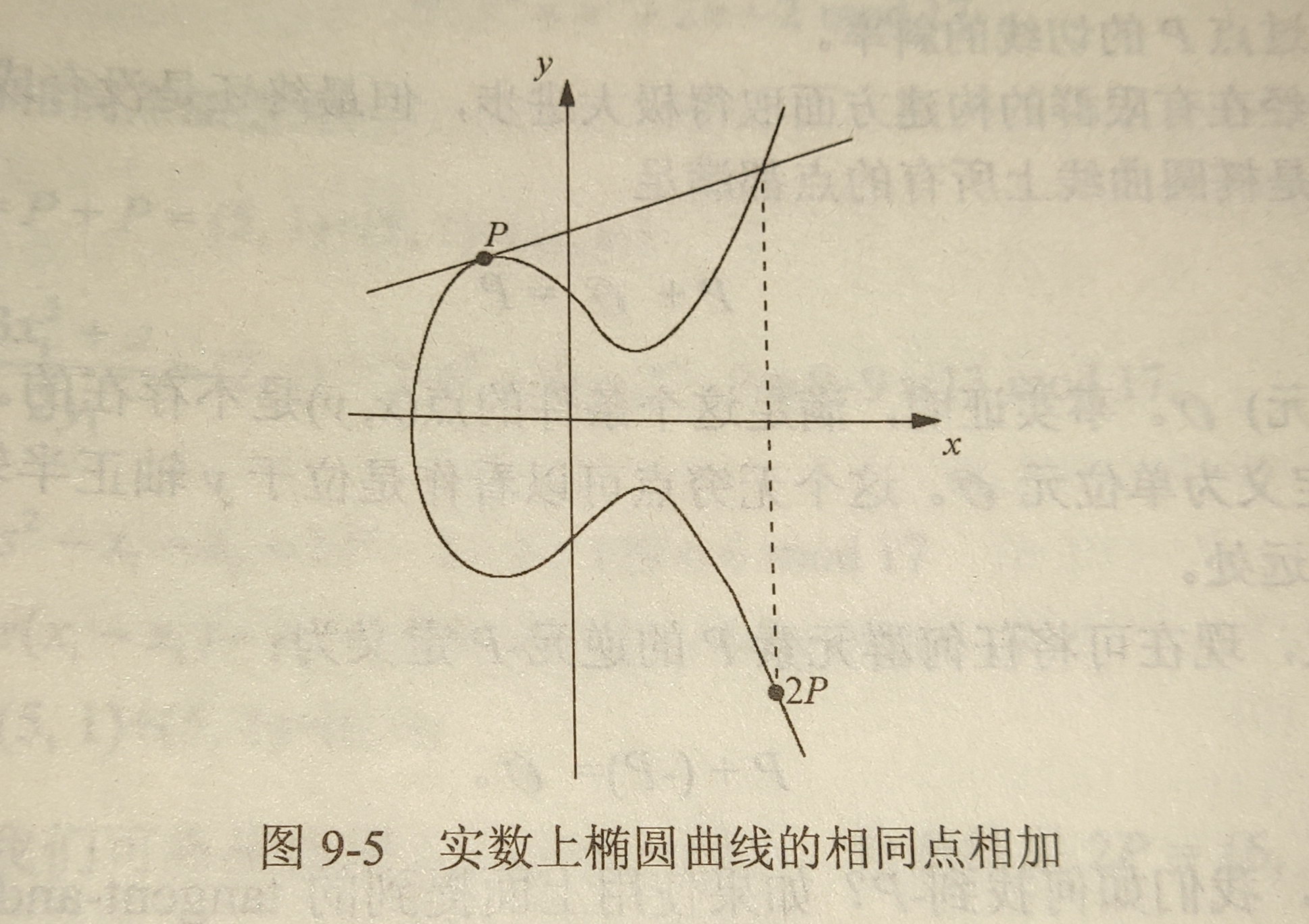
其坐标点的关系：

$$
x_3 = s^2 - x_1 - x_2;mod;p\
y_3 = s(x_1 - x_3) - y_1;mod;p\
;\
其中s的值会因情况不同而变化\
;\
s=\left{
\begin{array}{c}
\frac {y_2 - y_1}{x_2 - x_1};mod;p;;P≠Q\
\frac{3x^2_1 + a}{2y_1};mod;p;;P=Q
\end{array}
\right.
$$
注意：P + G =P P + (-P) = G

P(x_p , y_p)的逆元为-P(x_p , -y_p)，若在素数域上，则-P(x_p , P-y_p)

对于椭圆加密曲线的群操作，相当于把以前的群的数字变成了坐标点，群操作也只是变得稍微抽象了一些。

所以同样的，曲线上的点可以与G一起构成循环子群

假如一个群的阶数为X，那么X*P = G，（X+1）* P = P

相当于把之前的群的知识类比过来。

自然而然我们就可以构建出基于椭圆曲线的离散对数问题：

P + P + … +P = d*P =T

有了基于椭圆曲线的离散对数问题，我们自然也可以得到基于椭圆曲线的密钥交换：

基于椭圆加密曲线的密钥交换

ECDH域参数选取：

1.素数p和椭圆曲线：

​ y² ≡ x³ + a*x + b mod p

2.本原元P = (x_p , y_p) (此点可循环生成所有点)

椭圆曲线 Diffie-Hellman 密钥交换（ECDH）：

Alice: Bob:

选择k_prA = a ∈ {2,3,…,#E-1} 选择k_prB = b ∈ {2,3,…,#E-1}

计算k_pubA =aP =A = (x_A , y_A) 计算k_pubB = bP =B ∈(x_B , y_B)

​ A———–>

​ <————B

而后两人分别计算aB = T_AB , bA = T_AB

就得到了联合密钥：T（x_AB , y_AB）

（为了方便，图片都是从《深入浅出密码学》这本书上拍的，不过也推荐一下这本书。）