lfsr(线性反馈位移器)小结

lfsr拥有m个触发器和m个可能的反馈位置，系数p_i即反馈系数，s_i与p_i异或后（此处为一一对应异或），得到的一串新的序列，这一串序列再一一异或过去得到新的值也就是s_m,同时s₀会被输出，s_m会接替s_m-1的位置，整个序列相当于向前移了一个位置。

（感觉这样说不是很清楚，还是上公式吧）

s_m ≡ s_m-1p_m-1 + … + s₁p₁ + s₀p₀ mod 2(s_m = s_m-1p_m-1 ⊕ … ⊕ s₁p₁ ⊕ s₀p₀)

第m个元素会由此计算得出，第m+1个元素也很容易就可以推导出来：

s_m+1 ≡ s_mp_m-1 + … + s₂p₁ + s₁p₀ mod 2

m个触发器中的值会随着时间不断变化，但反馈系数不变，且新的值往往由之前的值决定。通过初始序列计算后来的序列自然是完全可以的，而通过后来的序列推算之前的序列也是可以的（如果知道反馈系数）

但即便不知道反馈系数，在特定条件下也可以进行攻击。

针对单个lfsr的已知明文攻击：

假设有明文x₀,x₁,…,x_2m-1,及其对应密文y₀,y₁,…,y_2m-1。我们便可以构造出初试的2m个序列：

s_i ≡ x_i + y_i mod 2 ; i=0,1,…,2m-1。

当我们拥有了2m个序列时，便可以很轻松地推出密钥k(即p_i),s_m由前m-1序列与k分别异或后再逐个异或而来，s_m+1同理，由此我们可以得到m个方程，未知数也是m个：

i=0, s_m ≡ s_m-1p_m-1 + … + s₁p₁ + s₀p₀ mod 2

i=1, s_m+1 ≡ s_mp_m-1 + … + s₂p₁ + s₁p₀ mod 2

… , …… …

i=m-1, s_2m-1 ≡ s_2m-2p_m-1 + … + p₁s_m + p₀s_m-1 mod2

就可以解出p_i 了。

这样看来lfsr是极易受到攻击的，所以我们往往组合使用。

Trivium

将三个位移寄存器结合使用，并借助AND操作提高了安全性。

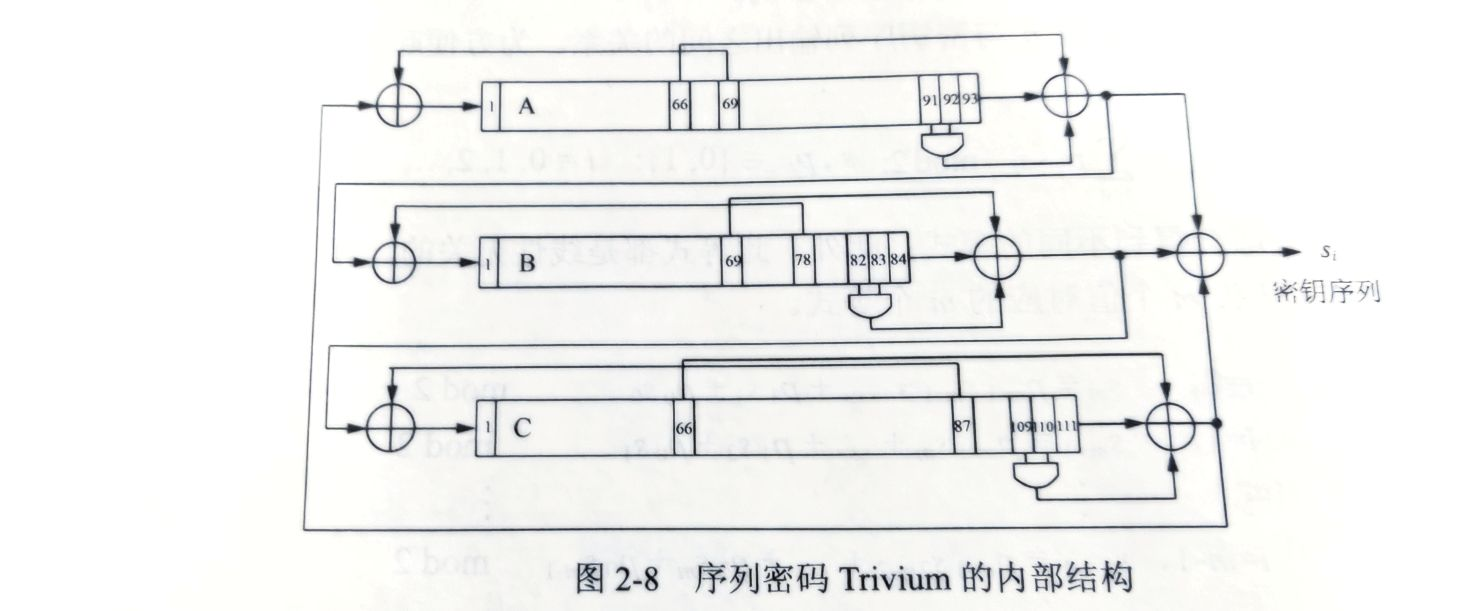
A位移反馈器长度为93，除去正常的位移器运行，69位会作为反馈为影响输入，66位则作为前馈位影响输出，同时91,92位进行AND操作与前馈位一起影响输出，而A的输出会作为B的输入的一部分，B的输出又会作为C的输入，而C的输出又将作为影响A的输入的一部分，而我们得到的密钥序列是A,B,C三个位移器的输出的异或值。

使用Trivium进行加密：

1.初始化阶段：将80位的iv加载至A,B最左边，C最右边3位为1，剩余都设置为0.

2.热身阶段：计时 4*288 = 1152次，并不输出。

3.加密阶段：至此开始产生的位构成密钥序列。

（热身阶段是为了充分随机化密码，确保密钥序列同时取决于密钥k和iv）